
Logaritmisk regression
Introduktion
Logaritmisk regression, dvs. linjens ligning for et sæt tal med en eksponentiel afhængighed, består af to elementer: selve funktionen der bestemmer a og b for funktionen y = b · ax, og en funktion der bestemmer R²-værdien, dvs. hvor godt talsættet passer med funktionen. Eksponentialfunktioner er ikke lineære funktioner, men ved afbildning med en logaritmisk akse (se næste afsnit), får man en ret linje, hvorfor man arbejder med den, som var den en ret linje med en skæring med y-aksen og en konstant hældning.
Bestemmelse af fremskrivningsfaktoren, a, og skæringen med y-aksen, b
Funktionen for logaritmisk regression, hvor man bestemmer fremskrivningsfaktoren og skæringen med y-aksen, eller y-interceptet som nogle kalder det, hedder LOGEST(). Har man en dansk version af Excel, hedder funktionen LOGREGR(). Ved brug af LOGEST() skal man være opmærksom på, at den anvender to celler ved siden af hinanden, dvs. man skriver funktionen i den ene celler og så bliver nabocellen til højre automatisk inddraget.
Ved anvendelse af LOGEST(), skal der i parantensen først angives f(x)-værdierne, og derefter de tilhørende x-værdier. De to talsæt adskilles med semikolon, dvs. LOGEST(f(x)-værdierne; x-værdierne). Værdierne der returneres er hhv. a og b for eksponentialfunktionen y = b · ax. Til LOGEST() er der også to valgfrie parametre, som tilføjes efter x-værdierne. Disse bliver gennemgået længere nede på siden.
I eksemplet med Excel nedenunder, kan man se koden som den er skrevet i celle E5. I celle F6 skriver Excel den samme kode, men den står her med grå skrift. Calc gør det lidt anderledes. Når man skriver koden og trykker enter, sætter Calc koden i krøllede paranteser og laver en kopi af dette i celle F6. Fordi Calc indsætter koden i to celler som et array, tillader Calc ikke at man redigerer eller sletter koden ved kun at redigere i den ene celle, som man normalt kan. Her skal man markere begge celler samtidig, før man kan komme til at redigere eller slette koden.
For Microsoft Excel ser det således ud:
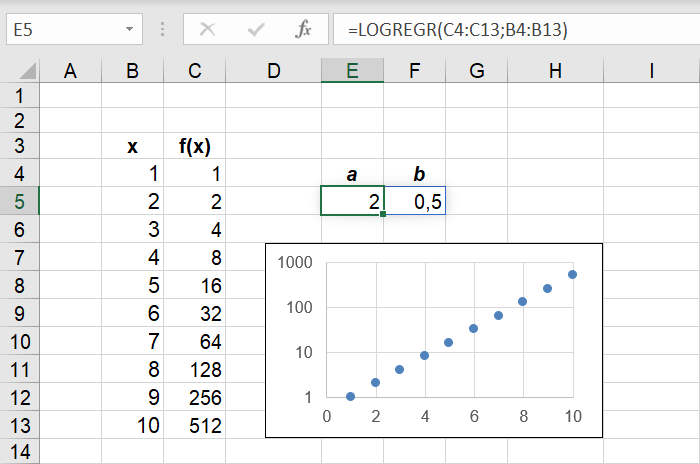
For OpenOffice Calc ser det således ud:
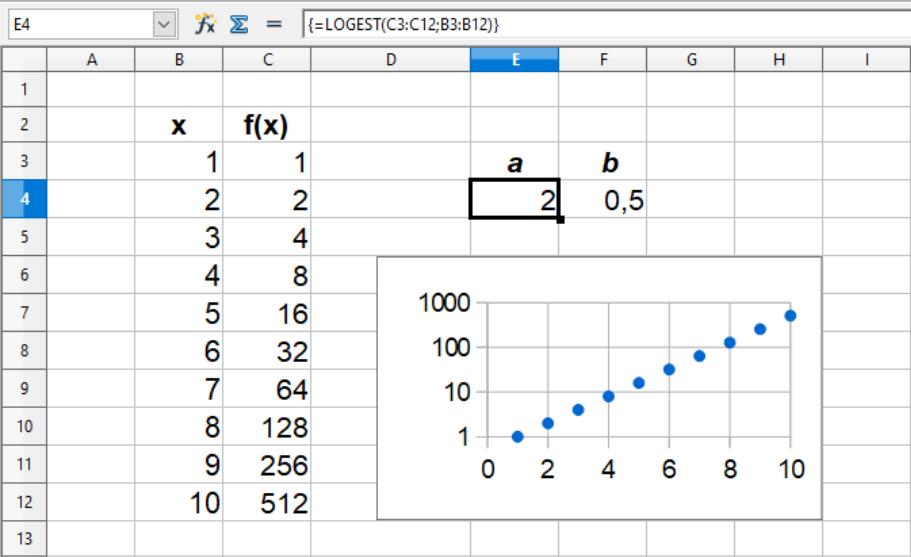
Ved anvendelse af LOGEST(), skal der i parantensen først angives f(x)-værdierne, og derefter de tilhørende x-værdier. De to talsæt adskilles med semikolon, dvs. LOGEST(f(x)-værdierne; x-værdierne). Værdierne der returneres er hhv. a og b for eksponentialfunktionen y = b · ax. Til LOGEST() er der også to valgfrie parametre, som tilføjes efter x-værdierne. Disse bliver gennemgået længere nede på siden.
I eksemplet med Excel nedenunder, kan man se koden som den er skrevet i celle E5. I celle F6 skriver Excel den samme kode, men den står her med grå skrift. Calc gør det lidt anderledes. Når man skriver koden og trykker enter, sætter Calc koden i krøllede paranteser og laver en kopi af dette i celle F6. Fordi Calc indsætter koden i to celler som et array, tillader Calc ikke at man redigerer eller sletter koden ved kun at redigere i den ene celle, som man normalt kan. Her skal man markere begge celler samtidig, før man kan komme til at redigere eller slette koden.
For Microsoft Excel ser det således ud:

For OpenOffice Calc ser det således ud:

R²-værdien
R²-værdien er et mål for hvor godt punkterne ligger på linje. For et datasæt hvor alt ligger helt på linje, vil R²-værdien være 1. Ved afvigelser giver det en lavere værdi.
For logaritmisk regression er der ikke en R²-funktion, på samme måde som man har RSQ() til den lineære regression. Man kan få den udregnet ved at bruge den udvidede LOGEST()-funktion, og på grafer kan man lave en trendline og få denne til at angive R²-værdien, men af uransagelige grunde er der ikke en specifik R²-funktion til logaritmisk regression.
For logaritmisk regression er der ikke en R²-funktion, på samme måde som man har RSQ() til den lineære regression. Man kan få den udregnet ved at bruge den udvidede LOGEST()-funktion, og på grafer kan man lave en trendline og få denne til at angive R²-værdien, men af uransagelige grunde er der ikke en specifik R²-funktion til logaritmisk regression.
Den udvidede LOGEST()-funktion
LOGEST() har to valgfrie parametre. I Excel hedder de const og stats (hhv. konstant og statistik hvis man har en dansk version af Excel). I Calc hedder de Function_type og stats. Med disse man kan lave lidt mere end bare at finde a og b for linjens ligning.
const/Function_type gør at man kan tvinge b-værdien til at være 1, dvs. linjen skal gå gennem (0,1). Her er der en forskel på Excel og Calc. Ved Excel bruger man TRUE hvis b skal bestemmes normalt (default) og FALSE, hvis linjen skal tvinges gennem (0,1). Har man en dansk version af Excel, bruger man SAND og FALSK. Ved Calc bruger man 0, hvis linjen skal tvinges gennem (0,1), og ved alle andre værdier (inklusiv ingen værdi) bestemmes b normalt (default). Calc synes her at acceptere alle tal, også negative tal og kommatal.
Med stats kan man lave yderligere regressionsstatistik, og her bliver det lidt kompliceret. For Excel kan man vælge TRUE, hvis man vil have den udvidede regressionsstatistik, og FALSE, hvis man ikke vil have den. FALSE er default. Har man en dansk version af Excel, bruger man SAND og FALSK. Ved Calc bruger man 0, man ikke vil have den udvidede regressionsstatistik (default), og ved alle andre værdier (inklusiv ingen værdi) får man den udvidede regressionsstatistik. Calc synes her at acceptere alle tal, også negative tal og kommatal. For overskuelighedens skyld bruger vi 1 her.
Når man vælger stats med de to regneark, får man blot fem rækker tal i to søjler, uden nogen form for angivelse af hvad de er, hvilket kan virke både forvirrende og uhensigtsmæssig. I de nedenstående eksempler er det anført ud for tallene, hvilke værdier der er tale om, så tallene giver mere mening.
For Microsoft Excel ser det således ud:
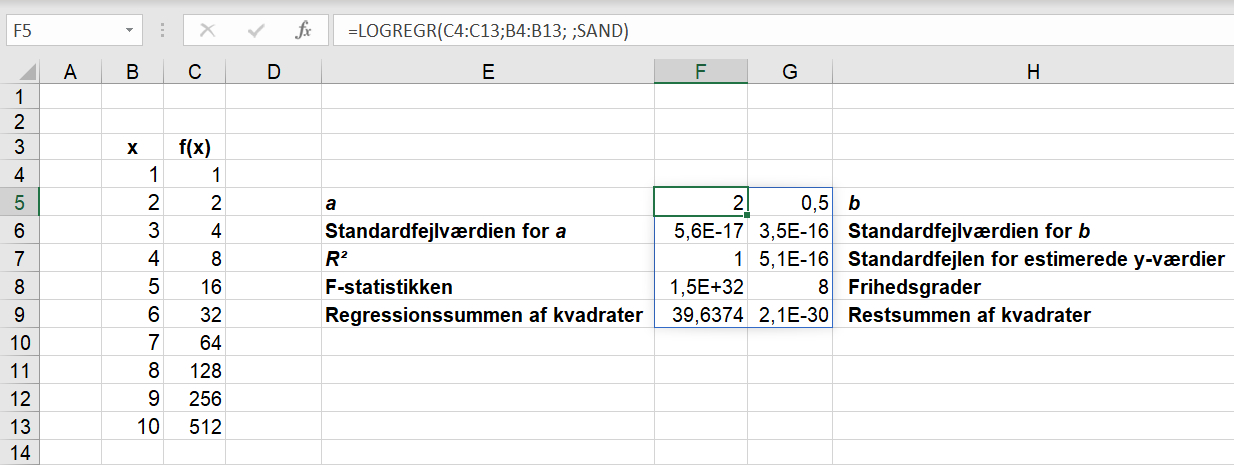
For OpenOffice Calc ser det således ud:
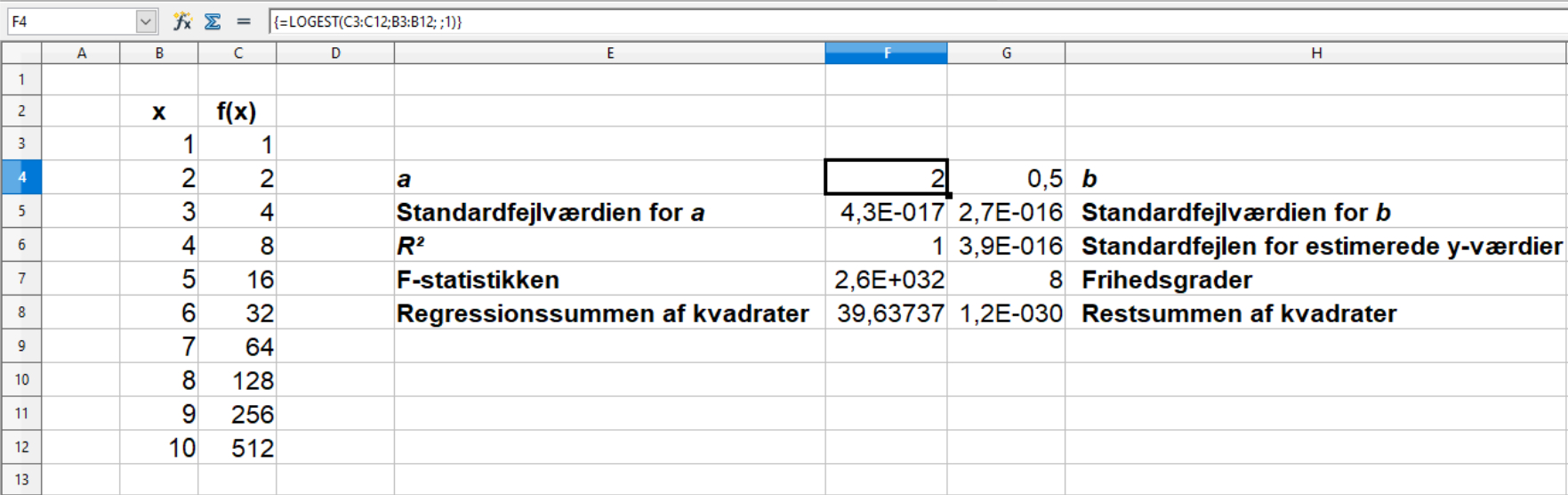
Bemærk, at der er ved de to regneark er forskellige værdier ved de ekstremt høje og ekstremt små værdier. Det er formodentligt forskelle i algoritmernes afrundinger i mellemregningerne.
const/Function_type gør at man kan tvinge b-værdien til at være 1, dvs. linjen skal gå gennem (0,1). Her er der en forskel på Excel og Calc. Ved Excel bruger man TRUE hvis b skal bestemmes normalt (default) og FALSE, hvis linjen skal tvinges gennem (0,1). Har man en dansk version af Excel, bruger man SAND og FALSK. Ved Calc bruger man 0, hvis linjen skal tvinges gennem (0,1), og ved alle andre værdier (inklusiv ingen værdi) bestemmes b normalt (default). Calc synes her at acceptere alle tal, også negative tal og kommatal.
Med stats kan man lave yderligere regressionsstatistik, og her bliver det lidt kompliceret. For Excel kan man vælge TRUE, hvis man vil have den udvidede regressionsstatistik, og FALSE, hvis man ikke vil have den. FALSE er default. Har man en dansk version af Excel, bruger man SAND og FALSK. Ved Calc bruger man 0, man ikke vil have den udvidede regressionsstatistik (default), og ved alle andre værdier (inklusiv ingen værdi) får man den udvidede regressionsstatistik. Calc synes her at acceptere alle tal, også negative tal og kommatal. For overskuelighedens skyld bruger vi 1 her.
Når man vælger stats med de to regneark, får man blot fem rækker tal i to søjler, uden nogen form for angivelse af hvad de er, hvilket kan virke både forvirrende og uhensigtsmæssig. I de nedenstående eksempler er det anført ud for tallene, hvilke værdier der er tale om, så tallene giver mere mening.
For Microsoft Excel ser det således ud:

For OpenOffice Calc ser det således ud:

Bemærk, at der er ved de to regneark er forskellige værdier ved de ekstremt høje og ekstremt små værdier. Det er formodentligt forskelle i algoritmernes afrundinger i mellemregningerne.